Page 19 - RMGO 3

Geometric constructions, with the compass alone, the straightedge alone or neither of them 19

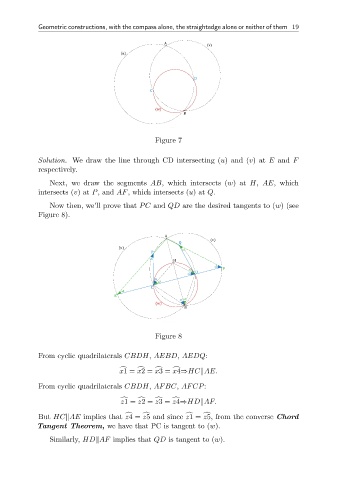
Figure 7

Solution. We draw the line through CD intersecting (u) and (v) at E and F
respectively.
Next, we draw the segments AB, which intersects (w) at H, AE, which
intersects (v) at P, and AF, which intersects (u) at Q.
Now then, we’ll prove that PC and QD are the desired tangents to (w) (see
Figure 8).

Figure 8

From cyclic quadrilaterals CBDH, AEBD, AEDQ:

x1 = x2 = x3 = x4⇒HCkAE.
c
c
c
c
From cyclic quadrilaterals CBDH, AFBC, AFCP:
z1 = z2 = z3 = z4⇒HDkAF.
c
c
c
c
But HCkAE implies that z4 = z5 and since z1 = z5, from the converse Chord
c
c
c
c
Tangent Theorem, we have that PC is tangent to (w).
Similarly, HDkAF implies that QD is tangent to (w).